Answer:
The probability that the fisher chosen from Clearwater did not have a license and the fisher chosen from Mountain View had a license is 0.32.
Explanation:
Denote the events as follows:
X = a fisher at Clearwater Park had a fishing license
Y = a fisher at Mountain View Park had a fishing license
The two events are independent.
The information provided is:
n (X) = 48
n (X') = 32
n (Y) = 72
n (Y') = 18
Then,
N (X) = n (X) + n (X')
= 48 + 32
= 80
N (Y) = n (Y) + n (Y')
= 72 + 18
= 90
Compute the probability that the fisher chosen from Clearwater did not have a license and the fisher chosen from Mountain View had a license as follows:
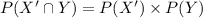
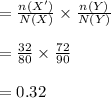
Thus, the probability that the fisher chosen from Clearwater did not have a license and the fisher chosen from Mountain View had a license is 0.32.