Question

Find the distance along an arc on the surface of the earth that subtends a central angle of 1 minutes (1 minute = 1/60 degree). The radius of the earth is 3960 miles. Round to the thousandths. (3 decimal places)

Answer 1

1.152 miles

Step-by-step explanation:

Given: central angle = 1 minute =
`((1)/(60)) ^(o)`

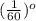
radius of the earth = 3960 miles

The length of an arc =
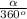`(\alpha )/(360^(o) )` 2
`\pi`r

where:
`\alpha` is the central angle, and r is the radius.

Thus,

Distance along the arc =
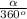`(\alpha )/(360^(o) )` 2
`\pi`r

Distance along the arc =
`(((1)/(60)) ^(o) )/(360^(o) )` x 2 x
`(22)/(7)` x 3960

=
`(((1)/(60)) ^(o) )/(360^(o) )` x 24891.4286

= 1.1524

The required distance along an arc is 1.152 miles.