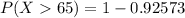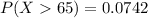Answer:
a
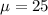
b
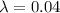
c
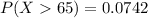
Explanation:
From the question we are told that
The number of success is n = 5
The time duration is N = 125 minutes
Generally the mean of the random variable is mathematically represented as

=>
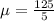
=>
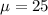
Generally the rate parameter is mathematically represented as
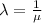
=>
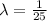
=>
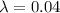
Generally the cumulative distribution function for exponential distribution function is
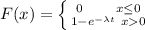
Generally the probability that the time to success will be more than 63 minutes is mathematically represented as
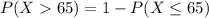
Here

=>
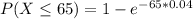
=>
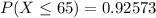
So