Answer:
The minimum cost for this number of passengers is Rs.36.05
Explanation:
The cost to build an amusement park ride by a certain contractor is represented by the function:
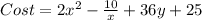
x : Number of people able to be on the ride at once.
Differentiate the function w.r.t x
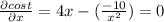
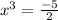
x=-1.3572
Differentiate the function w.r.t y
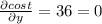
Minimum cost =
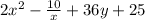
Minimum cost =

Minimum cost = 36.05
Hence the minimum cost for this number of passengers is Rs.36.05