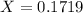Answer:
The value is
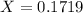
Explanation:
From the question we are told that
The entry fee is
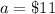
The outcome for first place is

The outcome for second place is
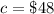
The outcome for losing is

The chance of finishing in the top two is X
Given that there are equal chance of finishing first or second, then the chance of finishing first is

and the chance of finishing second is

Then the chance of losing(i.e not finishing in the first two) is

given that the game is a fair gamble for the player as an expected maximizer then it mean is that the expected value of entering the tournament E(X) = 0
So
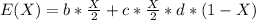
=>
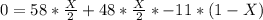
=>
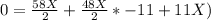
=>

=>