Answer: 0.038
Explanation:
Given: Total games : n= 375
Number of games won by the team that was winning the game at the end of the third quarter. = 300
The proportion (p) of the team that was winning the game at the end of the third quarter:
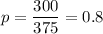
Critical z-value for 90% confidence: z* = 1.645
Margin of error =
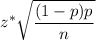
The margin of error in a 90% confidence interval estimate of p

Hence, the required margin of error = 0.038