Question

Find the absolute maximum and minimum values of the function below. f(x) = x3 − 9x2 + 3, − 3 2 ≤ x ≤ 12 Solution Since f is continuous on − 3 2 , 12 , we can use the Closed Interval Method. f(x) = x3 − 9x2 + 3 f ′(x) = 3x2−18x . Since f ′(x) exists for all x, the only critical numbers of f occur when f ′(x) = , that is, x = 0 or x = . Notice that each of these critical numbers lies in − 3 2 , 12 . The values

Answer 1

There are an absolute minimum (x = 6) and an absolute maximum (x = 12).

Explanation:

The correct statement is described below:

Find the absolute maximum and minimum values of the function below:

`f(x) = x^(3)-9\cdot x^(2)+ 3`,
`2 \leq x \leq 12`

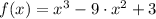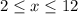
Given that function is a polynomial, then we have the guarantee that function is continuous and differentiable and we can use First and Second Derivative Tests.

First, we obtain the first derivative of the function and equalize it to zero:

`f'(x) = 3\cdot x^(2)-18\cdot x`

`3\cdot x^(2)-18\cdot x = 0`

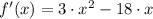
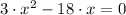
`3\cdot x \cdot (x-6) = 0` (Eq. 1)

As we can see, only a solution is a valid critical value. That is:
`x = 6`

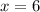
Second, we determine the second derivative formula and evaluate it at the only critical point:

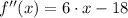`f''(x) = 6\cdot x -18` (Eq. 2)

x = 6

`f''(6) = 6\cdot (6)-18`

`f''(6) =18` (Absolute minimum)

Third, we evaluate the function at each extreme of the given interval and the critical point as well:

x = 2

`f(2) = 2^(3)-9\cdot (2)^(2)+3`

`f(2) = -25`

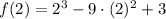
x = 6

`f(6) = 6^(3)-9\cdot (6)^(2)+3`

`f(6) = -105`

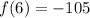
x = 12

`f(12) = 12^(3)-9\cdot (12)^(2)+3`

`f(12) = 435`

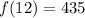
There are an absolute minimum (x = 6) and an absolute maximum (x = 12).