Question

A system has the same velocity profile but a depth of 10 feet. The average velocity of the stream with a depth of 10 feet is __________ the stream with a depth of 6 feet.

a. Greater than
b. Less tharn
c. The same as
d. The answer cannot be determined with the given information.

Answer 1

The average velocity of the stream with a depth of 10 feet is greater.

(a) is correct option.

Step-by-step explanation:

Given that,

Depth
`h_(1)= 10\ feet`

Depth
`h_(2)=6\ feet`

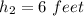
We need to calculate the average velocity of the stream

According to question,

`h_(1) > h_(2)`

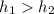
The velocity for first case,

`v_(1)=u_(1)(x_(1))/(h_(1))`

`(v_(1))/(x_(1))=(u_(1))/(h_(1))`

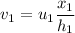
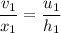
The velocity for second case,

`v_(2)=u_(2)(x_(2))/(h_(2))`

`(v_(2))/(x_(2))=(u_(2))/(h_(2))`

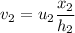
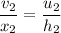
For the same velocity profile,

`(dv)/(dx)=(v_(1))/(x_(1))=(v_(2))/(x_(2))`

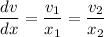
Then,

`(u_(1))/(h_(1))=(u_(2))/(h_(2))`

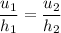
Put the value into the formula

`(u_(1))/(10)=(u_(2))/(6)`

`u_(1)=(5)/(3)u_(2)`

`u_(1)=1.67u_(2)`

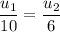
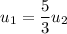
The velocity is
`u_(1) > u_(2)`

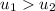
We need to calculate the average velocity for first case

Using formula of average velocity

`v_(avg)_(1)=(0+u_(1))/(2)`

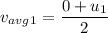
Put the value into the formula

`v_(avg)_(1)=(0+u_(1))/(2)`

`v_(avg)_(1)=(u_(1))/(2)`

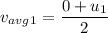
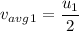
We need to calculate the average velocity for second case

Using formula of average velocity

`v_(avg)_(2)=(0+u_(2))/(2)`

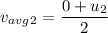
Put the value into the formula

`v_(avg)_(2)=(0+u_(2))/(2)`

`v_(avg)_(2)=(u_(2))/(2)`

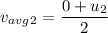
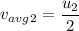
If
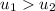`u_(1) > u_(2)` then
`(u_(1))/(2) >(u_(2))/(2)`

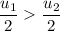
So, we can say that the average velocity of the stream with a depth of 10 feet will be greater than the stream with a depth of 6 feet.

Hence, The average velocity of the stream with a depth of 10 feet is greater.

(a) is correct option.