Answer:
A.
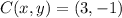 ,
,
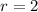 , x-Intercepts:
, x-Intercepts:
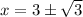 , y-Intercepts: none.
, y-Intercepts: none.
Explanation:
Let
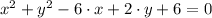 be the general equation of the circle, we must transform the expression into standard form to determine its center, radius and intercepts. The procedure is shown below:
be the general equation of the circle, we must transform the expression into standard form to determine its center, radius and intercepts. The procedure is shown below:
1)
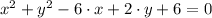 Given.
Given.
2)
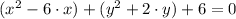 Commutative and associative properties.
Commutative and associative properties.
3)
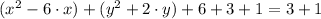 Compatibility with addition.
Compatibility with addition.
4)
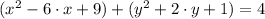 Definition of addition/Commutative and associative properties.
Definition of addition/Commutative and associative properties.
5)
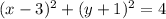 Perfect square trinomial/Result.
Perfect square trinomial/Result.
The equation of the circle centered in (h, k) in standard form is defined as:
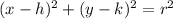 (Eq. 1)
(Eq. 1)
Where:
 ,
,
 - Coordinate of the center of the circle, dimensionless.
- Coordinate of the center of the circle, dimensionless.
 - Radius of the circle, dimensionless.
- Radius of the circle, dimensionless.
By direct comparison we find that circle is centered in
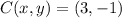 and has a radius of 2.
and has a radius of 2.
Finally, we obtain the intercepts of the given function:
x-Intercepts (
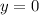 )
)
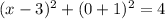
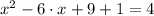
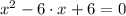
Roots are found analitically by Quadratic Formula:
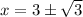
y-Intercepts (
 )
)
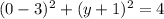
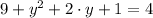

Roots are found analitically by Quadratic Formula:
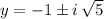
In a nutshell, there are no y-Intercepts.
We include a graphic including circle, center and x-Intercepts.
Finally, we came to the conclusion that correct answer is A.