Answer:
The ratio of the displacement amplitudes of two sound waves is 1.16.
Step-by-step explanation:
Given that,
Frequency = 5.0 kHz
Intensity level difference = 3.0 dB
We know that,
The sound intensity is inversely proportional to the square of distance.
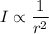
The sound intensity for first wave is
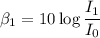 ...(I)
...(I)
The sound intensity for second wave is
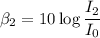 ...(II)
...(II)
We need to calculate the ratio of intensity
From equation (I) and (II)
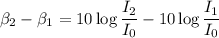
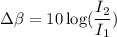
Put the value into the formula
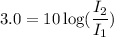
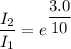
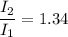
We need to calculate the ratio of the displacement
Using formula of displacement
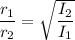
Put the value into the formula
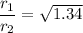
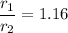
Hence, The ratio of the displacement amplitudes of two sound waves is 1.16.