Question

Kara and Nathan participated in a 60-minute maze race.

Kara:


32 minutes


Nathan:


40 minutes


Part B


Is the relationship in Part A rational or irrational? Justify your answer.


Select the answers that complete the sentences.


Hint(s): A rational number can be written as a ratio of two integers.


Can the times for each be written as integers?


The relationship is


The number


be expressed as a ratio of two integers.


1 rational


11 irrational


can


I cannot

Answer 1

A) There is a rational relationship, B) Given ratio is not an integer.

Explanation:

A) Is the relationship in Part A rational or irrational? Justifty your answer.

From Mathematics we remember that a rational number can formed by dividing a natural number by another natural number. Since Kara and Nathan had two natural numbers {32, 40} as their times of participation in the maze race, ratio between those times can be considered a rational number.

Hence, there is a rational relationship.

B) Can the times for each be written as integers?

The times represents the ratio of the upper number (40) to the lower number (32), the "times" can be written as integer if and only if denominator is equal to 1 after simplifying the ratio. That is:

`x = (40)/(32)`

`x = (20)/(16)`

`x = (10)/(8)`

`x = (5)/(4)`

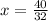
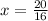
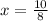
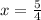
In consequence, this ratio does not represent an integer. (
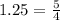`1.25=(5)/(4)`)