Answer:
The percentage of individuals from this population will have LDL levels 1 or more standard deviations above the mean is 16%.
Explanation:
Let X represent the LDL levels.
It is provided that
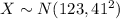 .
.
Compute the probability that a randomly selected individual is will have LDL levels 1 or more standard deviations above the mean as follows:
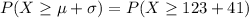
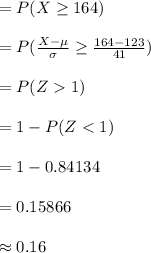
Thus, the percentage of individuals from this population will have LDL levels 1 or more standard deviations above the mean is 16%.