Question

Can someone help me know how to do this problem In finding what I can put in for (c) in order to get 2 imaginary solutions

Answer 1

To get 2 imaginary solutions, c must be less than -2

Explanation:

The general form of the quadratic equation is:

`ax^2+bx+c=0`

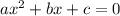
Solve the quadratic equation by using the formula:

`\displaystyle x=(-b\pm √(b^2-4ac))/(2a)`

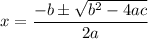
The equation to solve is:

`-2x^2+4x+c=0`

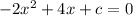
In our equation: a=-2, b=4, c=unknown

For the roots to be imaginary, the argument of the square root must be negative, that is:

`b^2-4ac<0`

Substituting the known values:

`4^2-4(-2)c<0`

`16+8c<0`

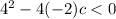
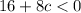
Subtracting 16:

`8c<-16`

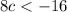
Solving:

`c<-2`

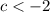
Thus, to get 2 imaginary solutions, c must be less than -2