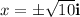What are the solutions to this quadratic equation? x^2+10=0

Question

asked Aug 20, 2021 55.9k views

2 Answers

Tono Kuriakose · Answer 1 · 2021-08-26T02:48:17+0000

Answer:

Correct choice: C.
$x=\pm√(10)\mathbf{i}$

Explanation:

The quadratic equation to solve is:

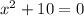
x^2+10=0

Since this equation is incomplete, we can solve it without using the quadratic solver formula.

Subtracting 10:

x^2=-10

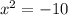
Taking square root:

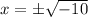
$x=\pm√(-10)$

Recall the square root of a negative number leads to imaginary solutions where the Unit Imaginary Number (i) is used, where:

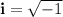
$\mathbf{i}=√(-1)$

The solutions to the equation are:

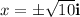
$x=\pm√(10)\mathbf{i}$

Correct choice: C.
$x=\pm√(10)\mathbf{i}$