Question

You and your cycling partner are capable of producing 955 W of power. What's the fastest you can pedal up a 4.90 ∘ slope if the combined mass of your tandem bicycle and both riders is 139 kg and you face a 14.5-N force from air resistance?

Answer 1

v= 7.3 m/s

Step-by-step explanation:

• Assuming that the cyclists are going uphill at constant speed, and neglecting friction between the tires and the road, the force exerted by the bikers must be equal and opposite to the force downhill.
• This force downhill, has two components, one due to gravity, and the other due to the air resistance.
• This last one is a given of the problem, 14.5 N.
• The force due to gravity along the slope of the road, can be showed that is as follows:

`F_(g) = m*g*sin\theta= 139 kg*9.8m/s2*sin 4.9 = 116.4 N`

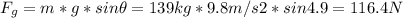
• So, the total force downhill is just the sum of the two:

`F_(net) =F_(g) + F_(air) = -130.9 N`

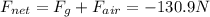
• (Taking as positive the direction uphill)
• Now, we know that the maximum power to be developed by the bikers, is P=955 W = 955 J/s
• As the power is energy per unit time, and the change in energy is equal to the work done, we can write the following expression:

`W = F* \Delta x = \Delta E = P*\Delta t`

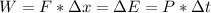
• As v = Δx/Δt, rearranging in the expression above, we get:
• P = F*v
• The force must be equal in magnitude and opposite to the one acting downhill, that we have just got, so as P is a given, we need just to solve for v, as follows:

`v_(max) = (P)/(F_(up) ) =(955 W)/(130.9N) = 7.3 m/s`

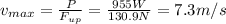
• So the fastest the bikers can climb the slope is 7.3 m/s.