Question

A golfer imparts a speed of 29.0 m/s to a ball, and it travels the maximum possible distance before landing on the green. the tee and the green are at the same elevation. (a) how much time does the ball spend in the air? (b) what is the longest hole in one that the golfer can make, if the ball does not roll when it hits the green?

Answer 1

Step-by-step explanation:

It is given that,

Initial speed of a golfer, u = 29 m/s

If it travels the maximum possible distance before landing. It means that it is projected at an angle of 45 degrees.

(a) We need to find the time spent by the ball in the air. It can be calculated by using second equation of motion.

`s=ut+(1)/(2)at^2`

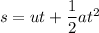
Here,

a = -g

s = 0 (it is displacement and it is equal to 0 as the ball lands on the green).

So,

`0=29\sin(45)t-(1)/(2)* 9.8t^2\ (\text{Initial vertical component of velocity is taken})\\\\-4.9t^2+29* (1)/(\sqrt2)t=0\\\\-4.9t^2+20.5t=0\\\\t=0,4.184\ s`

So, it will take 4.184 seconds in the air.

(b) let x is the longest hole in one that the golfer can make if the ball does not roll when it hits the green. It can be given by :

`x=vt\cos\theta\\\\x=29* 4.184* \cos(45)\\\\x=85.79\ m`

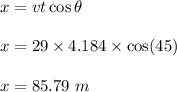
Hence, this is the required solution.