Question

A circular plate with radius 7 m is submerged vertically in water as shown. Express the hydrostatic force against one side of

the plate as an integral and evaluate it. (Round your answer to the nearest whole number. Use 9.8 m/s? for the
acceleration due to gravity. Recall that the mass density of water is 1000 kg/m²)
pg
XN
dy
х
3 m
m

Answer 1

`pg\int\limits^7_7(10-y)2√(7^2-y^2) \, dy`

*The last bound is negative 7

Then it equals 15085928 or 1.5E7

Explanation:

`x^2+y^2=7^2`

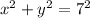
area = 2xdy

depth = (7+3)-y -> (10-y)

total force =
`pg\int\limits^7_7 {(10-y)2x} \, dy`

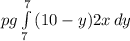
Substitute 2x from the first equation as x=
`√(7^2-y^2)`

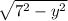
total force =
`pg\int\limits^7_7 {(10-y)2√(49-y^2) } \, dy`

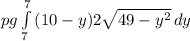
=pg1539.38

=(1,000)(9.8)(1539.38)=1.5E7 N

*Lower bound is -7, can't get the program to allow me to put it as a negative