Question

HELP ASAP DUE TOMORROW!!!

On a family outing, Tyler bought 5 cups of hot cocoa (x)
and 4 pretzels (y) for $18.40. Some of his family members
would like a second serving, so he went back to the same
food stand and bought another 2 cups of hot cocoa (x) and
4 pretzels (y) for $11.20.

Answer 1

Answers:

x = 2.40

y = 1.60

This means 1 hot cocoa costs $2.40 and 1 pretzel costs $1.60

=======================================

Work Shown:

x = cost of 1 cup of hot cocoa

y = cost of 1 pretzel

5x = cost of 5 cocoas

4y = cost of 4 pretzels

5x+4y = cost of 5 cocoas+4 pretzels

5x+4y = 18.40

----------------

2x = cost of 2 cocoas

4y = cost of 4 pretzels

2x+4y = cost of 2 cocoas+4 pretzels

2x+4y = 11.20

----------------

The system of equations we have is

`\begin{cases}5x+4y = 18.40\\2x+4y = 11.20\end{cases}`

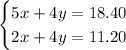
Note how 4y shows up twice. This is handy to be able to get rid of the y terms completely.

How? By subtracting the equations straight down

The x terms subtract to 5x-2x = 3x

The y terms subtract to 4y-4y = 0y = 0 and they go away

The right hand sides subtract to 18.40 - 11.20 = 7.20

After those three separate subtractions, we have this new equation:

3x = 7.20

Divide both sides by 3 to isolate x

3x/3 = 7.20/3

x = 2.40

Each hot cocoa costs $2.40

Now use this x value to find y. You can pick any equation you want as long as it has x,y in it. I'll pick the first equation

5x+4y = 18.40

5(2.40)+4y = 18.40

12+4y = 18.40

4y = 18.40-12

4y = 6.40

y = 6.40/4

y = 1.60

Each pretzel costs $1.60

If we picked on the second equation, we should get the same y value

Let's find out

2x+4y = 11.20

2(2.40)+4y = 11.20

4.80+4y = 11.20

4y = 11.20-4.80

4y = 6.40

y = 6.40/4

y = 1.60

We get the same result as before.

To check the answers, you need to plug those values back into the two original equations and simplify. You should get the same thing on both sides.