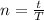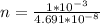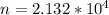Question

A medical cyclotron used in the production of medical isotopes accelerates protons to 6.5 MeV . The magnetic field in the cyclotron is 1.4 T . Part A What is the diameter of the largest orbit, just before the protons exit the cyclotron? Express your answer with the appropriate units. d d = nothing nothing SubmitRequest Answer Part B A proton exits the cyclotron 1.0 ms after starting its spiral trajectory in the center of the cyclotron. How many orbits does the proton complete during this 1.0 ms ? N N = nothing orbits SubmitRequest Answer Provide Feedback Next

Answer 1

a

The largest diameter is
`d =  0.523 \ m`

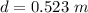
b

The number of revolution is
`n  =  2.132 *10^(4)`

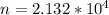
Step-by-step explanation:

From the question we are told that

The kinetic energy of the electron is
`K =  6.5 MeV =  6.5 *10^6 * 1.60 *10^(-19) = 1.04 *10^(-12) \  J`

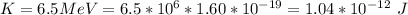
The magnetic field is
`B  =  1.4 \  T`

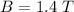
The time is
`t =  1 ms =  1*0^(-3) \  s`

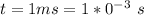
Generally the kinetic energy of the proton is mathematically represented as

`KE  =  (1)/(2)  *  m * v^2`

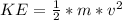
Here m is the mass of the proton with a value
`m = 1.672 *10^(-27) \  kg`

=>
`v  = \sqrt{ (2 *  K )/( m) }`

=>
`v  = \sqrt{ (2 *  1.04 *10^(-12)  )/( 1.672 *10^(-27)) }`

=>
`v  = 3.5271 * 10^(7) \  m/s`

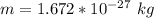
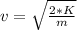
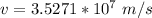
Generally the radius of the largest orbit is mathematically represented as

`r =  ( m *  v)/( B  *  e)`

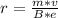
Here e is the charge on a proton with the value
`e =  1.60 *10^(-19) \  C`

`r =  ( 1.672 *10^(-27) * 3.5271 * 10^(7) )/(  1.4  *    1.60 *10^(-19) )`

=>
`r = 0.261 \ m`

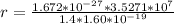
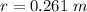
Generally the diameter is

`d =  2 *  r`

=>
`d =  2 *  0.261`

=>
`d =  0.523 \ m`

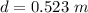
Gnerally the period of revolution round the orbit is mathematically represented as

`T  = (2 \pi  *  m )/(B  *  e)`

=>
`T  = (2 * 3.142  *  1.672 *10^(-27)  )/(1.4 *  1.60 *10^(-19))`

=>
`T  =  4.691 *10^(-8) \  s`

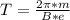
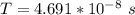
Generally the number of revolution is mathematically represented as

`n  =  (t)/(T)`

`n  =  (1*10^(-3))/(4.691 *10^(-8) )`

`n  =  2.132 *10^(4)`