Question

A cannonball has a speed of 320 m/s at an altitude of 122 m above the ground. What is the total mechanical energy of the cannonball assuming that the potential energy at ground level is zero

Answer 1

Each kilogram of the cannonball has a total energy of 52396.454 joules.

Step-by-step explanation:

From Principle of Energy Conservation we understand that energy cannot be destroyed nor created, but transformed. In this case non-conservative forces can be neglected, so that total energy of the cannonball (
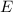`E`) is the sum of gravitational potential (
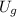`U_(g)`) and translational kinetic energies (
`K`), all measured in joules. That is:

`E = U_(g)+K` (Eq. 1)

By applying definitions of gravitational potential and translational kinetic energies, we proceed to expand the expression:

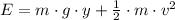`E = m\cdot g \cdot y + (1)/(2) \cdot m \cdot v^(2)` (Eq. 2)

Where:

`m` - Mass of the cannonball, measured in kilograms.

`g` - Gravitational acceleration, measured in meters per square second.

`y` - Height of the cannonball above ground level, measured in meters.

`v` - Speed of the cannonball, measured in meters per second.

As we do not know the mass of the cannonball, we must calculated the unit total energy (
`e`), measured in joules per kilogram, whose formula is found by dividing (Eq. 1) by the mass of the cannonball. Then:

`e = g\cdot y + (1)/(2)\cdot v^(2)`

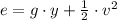
If we know that
`g = 9.807\,(m)/(s^(2))`,
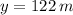`y =122\,m` and
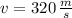`v = 320\,(m)/(s)`, the unit total energy of the cannonball is:

`e = \left(9.807\,(m)/(s^(2))\right)\cdot (122\,m)+(1)/(2)\cdot \left(320\,(m)/(s) \right)^(2)`

`e = 52396.454\,(J)/(kg)`

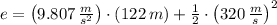
Each kilogram of the cannonball has a total energy of 52396.454 joules.