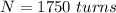Answer:
The number of turns is
Step-by-step explanation:
From the question we are told that
The inner radius is
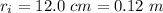
The outer radius is

The current it carries is
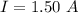
The magnetic field is
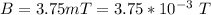
The distance from the center is
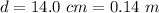
Generally the number of turns is mathematically represented as
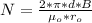
Generally
 is the permeability of free space with value
is the permeability of free space with value

So