Question

A boat, which moves at 12 miles per hour in water without a current, goes 45 miles upstream and 45 miles

back again in 8 hours. Find the speed of the current to the nearest tenth.
The speed of the current is
miles per hour.

Answer 1

Given:

Speed in still water = 12 miles per hour

Distance travel in upstream = 45 miles

Distance travel in downstream = 45 miles

Total time = 8 hours

To find:

The speed of current.

Solution:

Let the speed of current be x miles per hour.

Speed in upstream = (12-x) miles per hour

Speed in downstream = (12+x) miles per hour

We know that,

`Time=(Distance )/(Speed)`

Time to cover 45 miles in upstream =
`(45)/(12-x)`

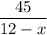
Time to cover 45 miles in downstream =
`(45)/(12+x)`

Total time is 8 hours. So,

`(45)/(12-x)+(45)/(12+x)=8`

`45\left ((1)/(12-x)+(1)/(12+x)\right)=8`

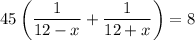
Taking LCM, we get

`45\left ((12+x+12-x)/(12^2-x^2)\right)=8`

`45\left ((24)/(144-x^2)\right)=8`

`(45* 24)/(8)=144-x^2`

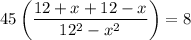
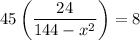
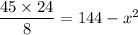
On further simplification, we get

`45* 3=144-x^2`

`135=144-x^2`

`x^2=144-135`

`x^2=9`

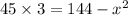
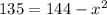
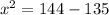
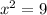
Taking square root on both sides.

`x=\pm √(9)`

`x=\pm 3`

Speed cannot be negative. So, x=3 only.

Therefore, the speed of the current is 3 miles per hour.