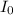Question

Two polaroids are placed at 90° to each other. What happens, when (n-1) more polaroids are inserted between them? Their axis are equally spaced. How does the transmitted intensity behave for large n?​

Answer 1

Step-by-step explanation:

hope it helps you

thank you

Answer 2

When (n-1) polaroids are placed between, two polaroids. Total number of polaroids becomes (n-1+1+1) = (n+1). The axis of all the polaroids are equally spaced. If x is angle between the axis of the two consecutive polaroids then:

`{:\implies \quad \sf x+x+x+\cdots \cdots n\:\:times=(\pi)/(2)}`

`{:\implies \quad \sf nx=(\pi)/(2)}`

`{:\implies \quad \sf x=(\pi)/(2n)}`

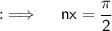
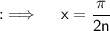
Now, by Malus law, we know that the intensity of light on passing through a pair of Polaroid is proportional to cos²(x). Before the light passes out of the last polaroid, this change in intensity will be repeated n times. If
`{I_0}` is intensity of the incident light and
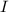`{I}`, is the intensity of light after passing through all the polaroids, then mathematically from Malus law:

`{:\implies \quad I=I_(0)\sf \cos^(2n)(x)}`

`{:\implies \quad I=I_(0)\sf \cos^(2n)\bigg((\pi)/(2n)\bigg)}`

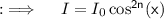
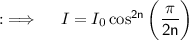
When, n will be very large, the angle x → 0, so that the whole cosine expression → 1. So, when n will be very much large,
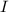`{I}` will approach
`{I_0}`