Answer:
4
Explanation:
Let the function given be f(x) = x³
The formula for calculating the average rate of change is expressed by:
f'(x) =
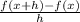
If f(x) = x³
f(x+h) = (x=h)³
substitute the functions in the formula
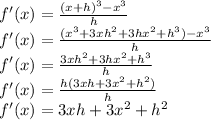
Since h = x₂-x₁ and x = 0
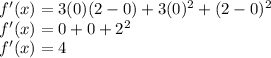
Hence the average rate of change is 4