Question

By definition, two rays labeled Ab and AC must exist with which of the following conditions?​

Answer 1

A. The two rays form angle CAB.

C. The two rays make a line AC.

D. The two rays intersect at point A.

E. The two rays are perpendicular.

This is shown in figure 1 in the attachment provided.

Explanation:

The given rays,
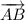`\overrightarrow{AB}` and
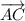`\overrightarrow{AC}` shows that both rays have a common endpoint A.

Therefore, the following conditions exists:

A. "The two rays form angle CAB."

Take a look at figure 1 in the attachment provided below. The two rays meet at point A to form angle CAB.

C. "The two rays make a line AC."

As shown in figure 2 in the attachment provided below, [
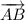`\overrightarrow{AB}` and
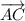`\overrightarrow{AC}` have a common end point, A, and they extend in opposite directions to form a straight line AC.
`(\overline{AC})`

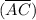
D. "The two rays intersect at point A."

This is shown in figure 1 in the attachment provided.

E. "The two rays are perpendicular."

Since
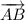`\overrightarrow{AB}` and
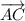`\overrightarrow{AC}` intersect at point A, they are perpendicular to each other, forming a right angle at point A. This we can see in figure 2 provided in the attachment.