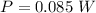Question

A horizontal spring-mass system has low friction, spring stiffness 163 N/m, and mass 0.3 kg. The system is released with an initial compression of the spring of 12 cm and an initial speed of the mass of 3 m/s. (a) What is the maximum stretch during the motion?

Answer 1

Complete Question

A horizontal spring-mass system has low friction, spring stiffness 163 N/m, and mass 0.3 kg. The system is released with an initial compression of the spring of 12 cm and an initial speed of the mass of 3 m/s.

(a) What is the maximum stretch during the motion?

(b) What is the maximum speed during the motion?

m/s

(c) Now suppose that there is energy dissipation of 0.02 J per cycle of the spring-mass system. What is the average power input in watts required to maintain a steady oscillation?

Answer:

a

`x_m  =  0.18 \  m`

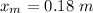
b

`v_m  =  4.10 \  m/s`

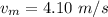
c

`P  = 0.085 \  W`

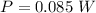
Step-by-step explanation:

From the question we are told that

The spring stiffness is
`k =  163 \  N/m`

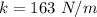
The mass is
`m  =  0.3 \  kg`

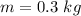
The initial compression is x = 12 cm = 0.12 m

The initial speed is v = 3 m/s

Generally the total energy stored in the spring at maximum stretch is equivalent to the kinetic energy and the energy stored at the initial compression

This can be mathematically represented as

`E_(max)  =  K  +  E_(i)`

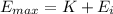
Here
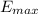`E_(max)` is the energy at maximum stretch which is mathematically represented as

`E_(max) =  (1)/(2) *  k  *  x_m^2`

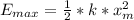
and

`E_(max) =  (1)/(2) *  k  *  x^2`

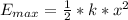
So

`(1)/(2) *  k  *  x_m^2 =  (1)/(2)m *  v^2   +  (1)/(2) *  k  *  x^2`

=>
`(1)/(2) *  163   *  x_m^2 =  (1)/(2)* 0.3 *   3^2   +  (1)/(2) *  163 *  0.12^2`

=>
`(1)/(2) *  163   *  x_m^2 =  (1)/(2)* 0.3 *   3^2   +  (1)/(2) *  163 *  0.12^2`

=>
`x_m  =  0.18 \  m`

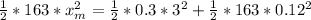
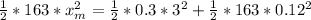
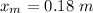
Gnerally the maximum kinetic energy when the stretch is zero(i.e during motion), according to the law of energy conservation, is equivalent to the kinetic energy when the spring is compressed plus the energy stored in the spring before it was released. , this can be mathematically represented as

`(1)/(2) *  k  *  x^2  + (1)/(2) *  m *  v^2  =  (1)/(2) * m * v_m ^2`

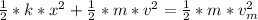
Here
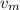`v_m` is the maximum velocity when the stretch is zero

So

`0.5 *  163   *  0.12^2  + (1)/(2) *  0.3 * 3^2  =  (1)/(2) * 0.3 * v_m ^2`

=>
`v_m  =  4.10 \  m/s`

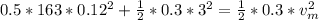
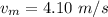
Generally the period of the spring is mathematically represented as

`T  =  2 *  \pi  *  \sqrt{(m)/(k) }`

=>
`T  =  2 *  3.142 *  \sqrt{(0.3)/(163) }`

=>
`T  =   0.2696 \  s`

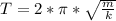
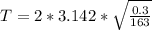
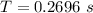
From the question we are told that the energy is 0.02 J

Generally the power is

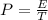
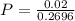
`P  =  (E)/(T)`

=>
`P  =  (0.02)/(0.2696)`

=>
`P  = 0.085 \  W`