Answer:
The wood was cut approximately 8679 years ago.
Explanation:
At first we assume that examination occured in 2020. The decay of radioactive isotopes are represented by the following ordinary differential equation:
 (Eq. 1)
(Eq. 1)
Where:
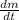 - First derivative of mass in time, measured in miligrams per year.
- First derivative of mass in time, measured in miligrams per year.
 - Time constant, measured in years.
- Time constant, measured in years.
 - Mass of the radioactive isotope, measured in miligrams.
- Mass of the radioactive isotope, measured in miligrams.
Now we obtain the solution of this differential equation:

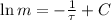
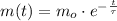 (Eq. 2)
(Eq. 2)
Where:
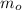 - Initial mass of isotope, measured in miligrams.
- Initial mass of isotope, measured in miligrams.
 - Time, measured in years.
- Time, measured in years.
And time is cleared within the equation:
![t = -\tau \cdot \ln \left[(m(t))/(m_(o)) \right]](https://img.qammunity.org/2021/formulas/mathematics/college/kdqzuj008qdgbz18axb8aggbcn5tiy3rgh.png)
Then, time constant can be found as a function of half-life:
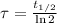 (Eq. 3)
(Eq. 3)
If we know that
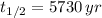 and
and
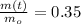 , then:
, then:
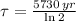
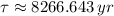
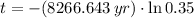
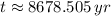
The wood was cut approximately 8679 years ago.