Question

A delivery truck travels 2.8 km North, 1.0 km East, and 1.6 km South. The final displacement from the origin is ___km to the ___.(round to the nearest tenth) (write the resultant vector as NE, SE, NW, or SW)

Answer 1

The final displacement from the origin is 1.6 km to the NE

Step-by-step explanation:

The directions in which the delivery truck travels are;

1) 2.8 km North = 2.8·
`\hat j`, in vector form

2) 1.0 km East = 1.0·
`\hat i`, in vector form

3) 1.6 km South = -1.6·
`\hat j`, in vector form

Therefore, to find the final displacement, Δx, of the delivery truck, we add the individual displacements as follows;

Final displacement, Δd = 2.8·
`\hat j` + 1.0·
`\hat i` +(-1.6·
`\hat j`) = 1.2·
`\hat j` + 1.0·
`\hat i`

Final displacement, = 1.0·
`\hat i` + 1.2·
`\hat j`

Where;

Δx = The displacement in the x-direction = 1.0·
`\hat i`

Δy = The displacement in the y-direction = 1.2·
`\hat j`

The magnitude of the resultant displacement vector is given as follows

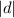`\left | d \right |` = √((Δx)² + (Δy)²) = √(1² + 1.2²) ≈ 1.6 (To the nearest tenth)

The magnitude of the resultant displacement vector ≈ 1.6 km

The direction of the resultant vector is positive for both the east and north direction, therefore, the direction of the resultant vector = NE

Therefore, the resultant displacement of the delivery truck is approximately 1.6 km, NE from the origin.