Complete Question:
Jamie used the distributive property to find the product of s(t) and h(t). His work was marked incorrect. Identify Jamie's mistake. What advice would you give Jamie to avoid this mistake in the future?
s(t)•h(t)= (3x-4)(2x-8)
= 6x² - 24x -8x - 32
= 6x² - 32x - 32
Answer:
Jamie made a mistake in his second line (6x² - 24x -8x - 32), by wrongly multiplying the operation signs. The last term should be +32, not -32.
Advice: Jamie should take note of the rule that applies when multiplying signs.
Step-by-step Explanation::
To find out where exactly Jamie made mistake, let's find the product of the given functions, step by step:
s(t)•h(t)= (3x-4)(2x-8)
Using distributive property, do the following:
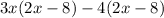

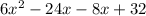 (this is where Jamie made mistake. -4 * -8 = +32. NOT -32.)
(this is where Jamie made mistake. -4 * -8 = +32. NOT -32.)
Add like terms
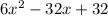
Jamie made a mistake in multiplying negative × negative. The last term in "6x² - 24x -8x - 32", should be +32. Negative × negative = +.
Therefore, it is advisable for Jamie to always take note of the rule that applies when multiplying signs.