Question

One of the wagers in roulette is to bet that the ball will stop on a number that is a multiple of 3. (Both 0 and 00 are not included.) If the ball stops on such a number, the player wins double the amount bet. If a player bets $5, compute the player's expectation. (Round your answer to two decimal places.)

Answer 1

The player's expectation is a loss of 20 cents.

Explanation:

In a game of roulette, there are 38 slots where the ball can stop.

The slots are numbered as follows: {0, 00, 1, 2, 3 ..., 36}.

So, N = 38.

The slots which are multiples of 3 are:

S = {3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33 and 36}

So, n (S) = 12.

Let X = the ball stops on a number that is a multiple of 3

The probability that the ball stops on a number that is a multiple of 3 is:

`P(X)=(n (S))/(N)=(12)/(38)=0.32`

It s provided that the player wins double the amount bet if the ball stops on a number that is a multiple of 3.

Compute the player's expectation as follows:

`E(X)=\sum X\cdot P(X)`

`=(\$10* 0.32)+(-\$5* (1-0.32))\\\\=\$3.20-\$3.40\\\\=-\$0.20`

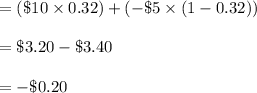
Thus, the player's expectation is a loss of 20 cents.