Question

What is the perimeter of the composite figure? Round to the nearest tenth

Answer 1

123.8 units

Explanation:

The vertices of the polygon has been labelled ABCDEF, as shown in the diagram attached below.

Perimeter of the Polygon =
`\overline{AB} + \overline{BC} + \overline{CD} + \overline{DE} + \overline{EF} + \overline{FA}`

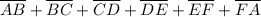
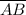`\overline{AB}` = |-12 - 24| = |-36| = 36 units

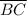`\overline{BC}`: calculate the distance between B(24, 16) and C(15, 3) using the distance formula.

`\overline{BC} = √((x_2 - x_1)^2 + (y_2 - y_1)^2)`

`\overline{BC} = √((24 - 15)^2 + (16 - 3)^2)`

`\overline{BC} = √((9)^2 + (13)^2)`

`\overline{BC} = √(81 + 169) = √(250)`

`\overline{BC} = 15.8 units`

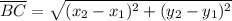
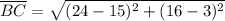
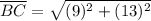
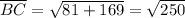
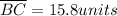
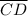`\overline{CD}` = |6 - 15| = |-9| = 9 units

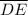`\overline{DE}` = |3 -(-12)| = |-15| = 15 units

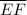`\overline{EF}` = |-12 - 6| = |-18| = 18 units

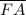`\overline{FA}` = |18 -(-12)| = 30 units

Perimeter = 36 + 15.8 + 9 + 15 + 18 + 30 = 123.8 units