Question

Below are the test scores for Ms. Brown's 1st and 2nd period math classes. Analyze the data and choose EACH correct statement:

1st period (Class A): 10, 15, 20, 25, 30, 35, 40

2nd period (Class B): 7, 12, 17, 25, 33, 38, 43

The standard deviation for Class A is 10

The standard deviation for Class B is 12.615

The mean (average) score for each class is the SAME.


The mean (average) score for each class is DIFFERENT.


The variance for Class A is 125.


The variance for Class B is 159.14.

choose each correct statement:

Class A has a greater spread.


Class B has a greater spread.


Based on the data, a score of 8 is more likely in Class B than Class A.


If graphed, Class B would look more like the red graph below and Class A would look more like the blue one.

Answer 1

The correct options are;

1) The mean (average) score for each class is the SAME

2) The variance of Class B is 159.14

3) Class B has a greater spread

4) Based on the data A score of 8 is more likely in class B than in class A

Explanation:

The given data are;

For the 1st period (Class A), we have

The mean, μ = (10 + 15 + 20 + 25 + 30 + 35 + 40)/7 = 175/7 = 25

The standard deviation σ, is given as follows;

`\sigma =\sqrt{(\sum \left (x_i-\mu \right )^(2) )/(N)}`

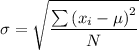
Where;

N = The number population size = 7

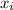`x_i` = The individual data values

Solving using Microsoft Excel formula STDEV.P gives, σ = 10

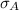`\sigma _A` ≈ 10

The variance = σ² = 10² = 100

For the 2nd period (Class B), we have

The mean, μ = (7 + 12 + 17 + 25 + 33 + 38 + 43)/7 = 175/7 = 25

The standard deviation σ, is given as follows;

`\sigma =\sqrt{(\sum \left (x_i-\mu \right )^(2) )/(N)}`

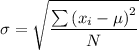
Where;

N = The number population size = 7

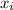`x_i` = The individual data values

Solving using Microsoft Excel formula STDEV.P gives,
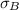`\sigma _B` ≈ 12.615

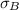`\sigma _B` ≈ 12.615 >
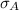`\sigma _A` ≈ 10, class B has greater spread

The variance = σ² = 12.615² ≈ 159.14

A score of 8 is more likely in class B than in class A due to the availability of data before and after the a score of 8