Question

Decide whether the experiment is a binomial experiment:

A. Selecting five cards, one at a time without replacement, from a standard deck of cards. The random variable is the number of face cards obtained.
B. Survey 50 investors to see how many different stocks they own. The random variable represents the number of different stocks owned by each investor.
C. Survey 150 college students to see whether they are enrolled as new students. The random variable represents the number of students enrolled as a new student.
D. Each week, a gambler plays blackjack at the local casino. The random variable is the number of times per week the player wins.

Answer 1

The correct options are A and C.

Explanation:

A Binomial experiment has the following properties:

• There are a fixed number of trials (n).
• Each trial are independent of the others.
• Each trial has only two outcomes: Success and Failure
• Each trial has the same probability of success (p).

If a random variable X is used in an experiment and the experiment has all the above mentioned properties, then the random variable X is known as a binomial random variable.

(A)

Selecting five cards, one at a time without replacement, from a standard deck of cards. The random variable is the number of face cards obtained.

X = number of face cards .

There are n = 52 cards in a standard deck of cards.

There are 12 face cards in the standard deck of cards.

The probability of selecting a face card is,
`p=(12)/(52)=0.231`.

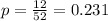The selection is done without replacement.

Thus, the experiment is a binomial experiment.

(C)

Survey 150 college students to see whether they are enrolled as new students. The random variable represents the number of students enrolled as a new student.

X = number of students enrolled as a new student.

The number of students selected for the survey, n = 150.

Each students response is independent of the others.

Thus, the experiment is a binomial experiment.