Question

Which series of transformations shows that figures 1 and 2 are similar?

Figure 1 is the preimage. *
sty
7
6
5
AU
2
1
O
3
--7-6-5-4-3 2-1
4 5 6 7 8
-5
-6
-7
-81
о
a dilation of figure 1 with scale factor 12 then a reflection
О
a dilation of figure 1 with scale factor 12 then a translation
a dilation of figure 1 with scale factor 3/2 then a translation
a dilation of figure 1 with scale factor 3/2 then a reflection

Answer 1

Option (4)

Explanation:

Length of segment between two points
`(x_1,y_1)` and
`(x_2,y_2)` is given by,

d =
`√((x_2-x_1)^2+(y_2-y_1)^2)`

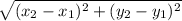
From the figure attached,

Distance between A(0, -3) and B(3, 0) =
`√((3-0)^2+(0+3)^2)`

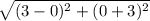
AB =
`3√(2)`

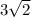
Distance between A'(-3.5, -4.5) and B'(-8, 0)

Length of A'B' =
`√((-3.5+8)^2+(-4.5-0)^2)`

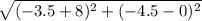
A'B' =
`4.5√(2)`

Scale factor for dilation =
`(4.5√(2))/(3√(2))=1.5`

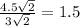
Therefore series of transformations will be,

A dilation of figure 1 with scale factor of
`(3)/(2)` and then a reflection.

Option (4) will be the answer.