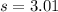Answer:
The probability distribution of x is
Profits in millions (x) Probability of getting contract (P(x))
$10 0.15
$ 5 0.30
$ 2 0.45
$ 0 0.10
The mean is
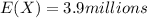
The standard deviation is
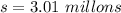
Explanation:
Generally the probability distribution of x is
Profits in millions (x) Probability of getting contract (P(x))
$10 0.15
$ 5 0.30
$ 2 0.45
$ 0 0.10
Generally the mean is mathematically represented as
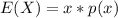
=>
![E(X) = [10 * 0.15 ] + [5 *0.30 ] + [2 * 0.45 ] + [0 * 0.10]](https://img.qammunity.org/2021/formulas/mathematics/college/lp56ajminqw37yt16o7967ql6492ypifw2.png)
=>
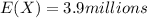
Now
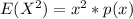
=>
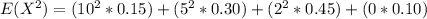
=>
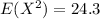
Gnerally the variance is mathematically represented as
![V(X) = E(X^2) - [E(X)]^2](https://img.qammunity.org/2021/formulas/mathematics/college/n7ttfgvxlty4g6jtmhze20f1ks1imqakzo.png)
=>
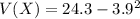
=>
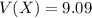
Gnerally the standard deviation is mathematically represented as
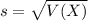
=>
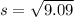
=>