Complete Question
A political analyst believes that a senator's recent decision to support a bill resulted in a drop of approval ratings. To test this claim, he selects random cities in the state the senator represents and compares the approval ratings before the decision to the approval ratings after the decision. Suppose that data were collected for a random sample of 8 cities, where each difference is calculated by subtracting the percent approval rating before the decision from the percent approval rating after the decision. Assume that the ratings are normally distributed. Using a test statistic oft -3.935, the significance level Q=0.05, and the corresponding p-value less than 0.01, draw a conclusion for the appropriate hypothesis test, where the null hypothesis is
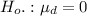 and the alternative hypothesis is
and the alternative hypothesis is
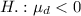
a. Reject the null hypothesis.
b. Fail to reject the null hypothesis.
c. The conclusion of the hypothesis test is that there is sufficient evidence to suggest that there was a drop in approval ratings in cities after the decision to support the bill.
d. The conclusion of the hypothesis test is that there is insufficient evidence to suggest that there was a drop in approval ratings in cities after the decision to support the bill.
Answer:
The correct option is a and c
Explanation:
From the question we are told that
The sample size is n = 8
The test statistics is t = -3.935
The level of significance is

The p-value is
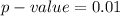
From the data given we see that the
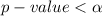 hence
hence
The decision rule is
Reject null hypothesis
The conclusion
There is sufficient evidence to suggest that there was a drop in approval ratings in cities after the decision to support the bill.