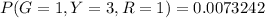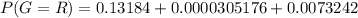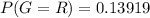Answer:
a
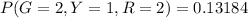
b
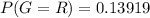
Explanation:
From the question we are told that
The probability of the traffic light being green is
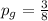
The probability of the traffic light being red is

The probability of the traffic light being yellow is
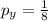
The number of days of observation is n = 5
Generally the probability distribution function for a multinomial distribution is mathematically represented as

Generally the probability that P[G=2, Y=1, R=2]
![P(G = 2 , Y= 1 , R = 2) = (5!)/( 2! * 1! * 2!) * [(3)/(8) ]^2 * [(1)/(8) ]^1 * [(1)/(2) ] ^2](https://img.qammunity.org/2021/formulas/mathematics/high-school/qg8vxhe53aptig5tzgq5vjvfr2x7qyyx8i.png)
=>
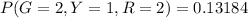
Generally the probability that P[G=R] is mathematically represented as
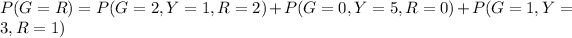
Here
![P( G = 0 , Y = 5 , R = 0) = (5!)/( 0! * 5! * 0!) * [(3)/(8) ]^0 * [(1)/(8) ]^5 * [(1)/(2) ] ^0](https://img.qammunity.org/2021/formulas/mathematics/high-school/bfy8vab7ci1t6m2nmnmuldwe1agpq11y15.png)

Also
![P( G = 1 , Y = 3 , R = 1)= (5!)/( 1! * 3! * 1!) * [(3)/(8) ]^1 * [(1)/(8) ]^3 * [(1)/(2) ] ^1](https://img.qammunity.org/2021/formulas/mathematics/high-school/766dmxe2mpx2gxbaab1lh7al7ur22tk87i.png)