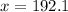Answer:
a
P(X \le 250 ) = 0.7564 [/tex] ,
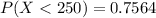 ,
,
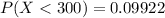
b

c
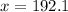
Explanation:
From the question we are told that
The value for

The value for
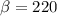
Generally the Weibull distribution function is mathematically represented as
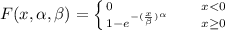
Generally the probability that a specimen's lifetime is at most 250 is mathematically represented as
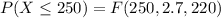
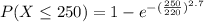
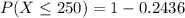

Generally the probability that a specimen's lifetime is less than 250
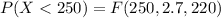
[texP(X < 250 ) =1 - e^{- (\frac{250}{220} )^{2.7}}[/tex]
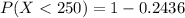
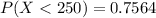
Generally the probability that a specimen's lifetime is more than 300
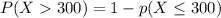
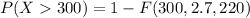
[texP(X < 300) =1- [1 - e^{- (\frac{300}{220} )^{2.7}}][/tex]
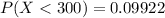
Generally the probability that a specimen's lifetime is between 100 and 250 is
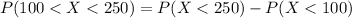
=>
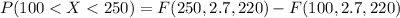
=>
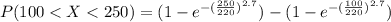
=>
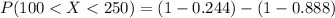
=>

Generally the value such that exactly 50% of all specimens
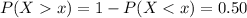
=>
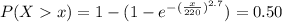
=>
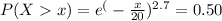
=>
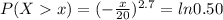
=>
![P(X> x ) = (x)/(20) =[ -ln0.50 ] ^{frac{1}{2.7}}](https://img.qammunity.org/2021/formulas/mathematics/high-school/o43wcg0npgflyxsrv517abmtzq2u26bwk9.png)
=>
![x = 220[ -ln0.50 ] ^{frac{1}{2.7}}](https://img.qammunity.org/2021/formulas/mathematics/high-school/aivl7xucbwxgu74woxo5o4pq0ilejetstg.png)
=>