(1) f(x) = (1 - x³) / (x - 1)
(a) The domain is the set of values that this function can take on. If x = 1, the denominator becomes 0 and the function is undefined. Any other value of x is okay, though, since for x ≠ 1, we have
f(x) = (1 - x³) / (x - 1) = - (1 - x³) / (1 - x) = -(x² + x + 1)
which is defined for all x. This also tells us that the plot of f(x) is a parabola with a hole at x = 1. So, the domain is the interval (-∞, 1) ∪ (1, ∞).
(b) The range is the set of values that the function actually does take on. Taking the simplified version of f(x), we can complete the square to write
-(x² + x + 1) = -(x² + x + 1/4 - 1/4) - 1 = -(x + 1/2)² - 3/4
which is represented by a parabola that opens downward, with a maximum value of -3/4. So the range is the interval (-∞, -3/4).
(c) Judging by the plot of f, the limits at both negative and positive infinity are -∞.
(d) Same answer as part (a).
(2) f(x) = x³ - x
(a) The derivative of f at x = 3, and hence the slope of the tangent line to this point, is
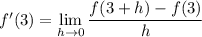
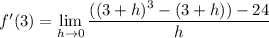
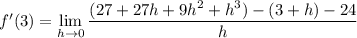
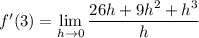
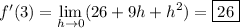
(b) The tangent line at x = 3 has equation
y - f (3) = f ' (3) (x - 3)
y - 24 = 26 (x - 3)
y = 26 x - 54
We also want to find any other tangent lines parallel to this one, which requires finding all x for which f '(x) = 26. We could use the same limit definition as in part (a), but to save time, we exploit the power rule to get
f '(x) = 3 x² - 1
Then solve for when this is equal to 26:
3 x² - 1 = 26 ==> x² = 9 ==> x = ±3
The other tangent line occurs at x = -3, for which we have f (-3) = -24, and so the equation for the tangent is
y - f (-3) = 26 (x - (-3))
y + 24 = 26 (x + 3)
y = 26 x + 54