Question

The lifetime in months of a transistor in a certain application is random with probability density function:

f(x) = {0.4e^-0.4x, x>0 0, x<0


a. Compute the mean lifetime.

b. Compute the standard deviation of the lifetimes.

c. Compute the cumulative distribution function of the lifetime.

d. Compute the probability that the lifetime will be less than 6 months.

e. Compute the 60^th percentile of the lifetime.

Answer 1

Explained below.

Explanation:

The probability density function of lifetime in months of a transistor in a certain application is:

`f(x)=0.4\cdot e^(-0.4x);x>0`

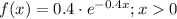
The probability density function suggests that the random variable X follows a exponential function with parameter λ = 0.4.

(a)

Compute the mean lifetime as follows:

`\mu=(1)/(\lambda)=(1)/(0.40)=2.5`

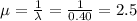
Thus, the mean lifetime is 2.5 months.

(b)

Compute the standard deviation of the lifetimes as follows:

`\sigma=\sqrt{(1)/(\lambda^(2))}=\sqrt{(1)/(0.40^(2))}=2.5`

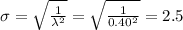
Thus, the standard deviation of the lifetimes is 2.5 months.

(c)

The cumulative distribution function of the lifetime is:

`CDF=1-e^(-0.40x)`

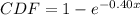
(d)

Compute the probability that the lifetime will be less than 6 months as follows:

`P(X<6)=\int\limits^(6)_(0) {0.40\cdot e^(-0.40x)} \, dx`

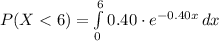
`=0.40* [(e^(-0.40x))/(-0.40)]^(6)_(0)\\\\=-1* [e^(-0.40*6)-e^(-0.40*0)]\\\\=-0.090718+1\\\\=0.909282\\\\\approx 0.9093`

Thus, the probability that the lifetime will be less than 6 months is 0.9093.

(e)

Compute the 60th percentile of the lifetime as follows:

`P(X<x)=0.60\\\\\int\limits^(x)_(0) {0.40\cdot e^(-0.40x)} \, dx=0.60\\\\0.40* [(e^(-0.40x))/(-0.40)]^(x)_(0)=0.60\\\\-1* [e^(-0.40* x)-e^(-0.40*0)]=0.60\\\\1-e^(-0.40x)=0.60\\\\e^(-0.40x)=0.40\\\\-0.40x=\ln(0.40)\\\\-0.40x=-0.916291\\\\x=2.2907275\\\\x\approx 2.3`

Thus, the 60th percentile of the lifetime is 2.3 months.