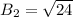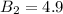Answer:
4.9 feet
Explanation:
First, we need to determine the height of the building using the following:
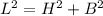
Where
H = Height of the building
L = Length of the first ladder = 20ft
B = Distance from the base of the building = 10ft
So, we have:
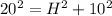

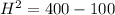
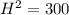

Next, is to determine the distance of the new ladder from the base of the building (B) using Pythagoras theorem using:

Where
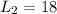 --- Length of the second ladder
--- Length of the second ladder
 ----- Height of the building
----- Height of the building
So, we have:

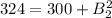
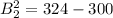
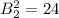
Solving for B2, we have: