Question

Winners of the Georgia Lotto drawing are given the choice of receiving the winning amount divided equally over 19 years or as a​ lump-sum cash option amount. The cash option amount is determined by discounting the annual winning payment at 8​% over 19 years. This week the lottery is worth ​$3 million to a single winner. What would the cash option payout​ be?

Answer 1

$615,304.33

Step-by-step explanation:

In order to solve this, we need to use the compound interest formula to calculate the final amount after deducting the 8% for 19 years. The formula is the following...

`A = P(1 + (r)/(n) )^(nt)`

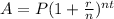
Where:

A = the future value of the investment/loan, including interest

P = the principal investment amount (the initial deposit or loan amount)

r = the annual interest rate (decimal)

n = the number of times that interest is compounded per unit t

t = the time the money is invested or borrowed for

Now we plug in the values and solve for A

`A = P(1 + (r)/(n) )^(nt)`

`A = 3000000(1 + (-0.08)/(1) )^((1)(19))`

`A = 3000000(0.92 )^(19)`

`A = 3000000 * 0.2051`

`A = 615,304.33`

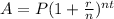
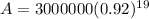
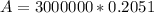
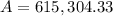
Therefore, the final lump sum payout would be $615,304.33