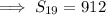Answer:
912
Explanation:
Sum of the first n terms of an arithmetic series:
![S_n=\frac12n[2a+(n-1)d]](https://img.qammunity.org/2023/formulas/mathematics/high-school/rprbqmnhjd3ubi2oep6cnn7sulqx9s9epc.png)
where:
- n = nth term
- a = first term
- d = common difference
Given arithmetic series: 3 + 8 + 13 + 18 + ...
Therefore:
To find the sum of the first 19 terms, substitute the given values together with n = 19 into the Sum formula:
![\implies S_(19)=(1)/(2)(19)\left[\:2(3)+5(19-1)\:\right]](https://img.qammunity.org/2023/formulas/mathematics/college/norhfmrk1yghtqfay00ui9ctst57lqdv9e.png)
![\implies S_(19)=(19)/(2)\left[\:6+90\:\right]](https://img.qammunity.org/2023/formulas/mathematics/college/k63gwqpygo0huoeoc4f719ojm4640adsye.png)
![\implies S_(19)=(19)/(2)\left[\:96\:\right]](https://img.qammunity.org/2023/formulas/mathematics/college/4zuy68d9nat7493wmuid2tfo71ypc61xkv.png)