The distance between the points (2, 3) and (-2, -1) on the coordinate plane is approximately 5.7 units when rounded to the nearest tenth.
How to find the distance of two points on a coordinate plane?
To find the distance (d) between two points
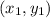 and
and
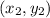 on the coordinate plane, you can use the distance formula:
on the coordinate plane, you can use the distance formula:
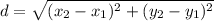
For the points (2, 3) and (-2, -1):
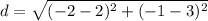
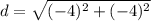
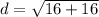
d = √32
d ≈ 5.7
Therefore, the distance between the two points is approximately 5.7 units when rounded to the nearest tenth.