Question

the height h(t) of a trianle is increasing at 2.5 cm/min, while it's area A(t) is also increasing at 4.7 cm2/min. at what rate is the base b(t) chaging when the height h=15cm and the area A= 130cm2

Answer 1

The base of the triangle decreases at a rate of 2.262 centimeters per minute.

Explanation:

From Geometry we understand that area of triangle is determined by the following expression:

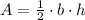`A = (1)/(2)\cdot b\cdot h` (Eq. 1)

Where:

`A` - Area of the triangle, measured in square centimeters.

`b` - Base of the triangle, measured in centimeters.

`h` - Height of the triangle, measured in centimeters.

By Differential Calculus we deduce an expression for the rate of change of the area in time:

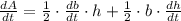`(dA)/(dt) = (1)/(2)\cdot (db)/(dt)\cdot h + (1)/(2)\cdot b \cdot (dh)/(dt)` (Eq. 2)

Where:

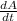`(dA)/(dt)` - Rate of change of area in time, measured in square centimeters per minute.

`(db)/(dt)` - Rate of change of base in time, measured in centimeters per minute.

`(dh)/(dt)` - Rate of change of height in time, measured in centimeters per minute.

Now we clear the rate of change of base in time within (Eq, 2):

`(1)/(2)\cdot(db)/(dt)\cdot h = (dA)/(dt)-(1)/(2)\cdot b\cdot (dh)/(dt)`

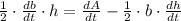
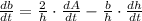`(db)/(dt) = (2)/(h)\cdot (dA)/(dt) -(b)/(h)\cdot (dh)/(dt)` (Eq. 3)

The base of the triangle can be found clearing respective variable within (Eq. 1):

`b = (2\cdot A)/(h)`

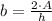
If we know that
`A = 130\,cm^(2)`,
`h = 15\,cm`,
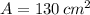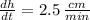`(dh)/(dt) = 2.5\,(cm)/(min)` and
`(dA)/(dt) = 4.7\,(cm^(2))/(min)`, the rate of change of the base of the triangle in time is:

`b = (2\cdot (130\,cm^(2)))/(15\,cm)`

`b = 17.333\,cm`

`(db)/(dt) = \left((2)/(15\,cm)\right)\cdot \left(4.7\,(cm^(2))/(min) \right) -\left((17.333\,cm)/(15\,cm) \right)\cdot \left(2.5\,(cm)/(min) \right)`

`(db)/(dt) = -2.262\,(cm)/(min)`

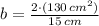
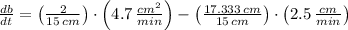
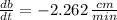
The base of the triangle decreases at a rate of 2.262 centimeters per minute.