Answer:
A & B
Explanation:
See attachment for complete question
Given

Analyzing the given options
Option A:
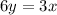
Divide both sides by 6
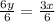
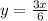

This is true for the given expression:
Option B:
From the graph:
x = 2, when y = 1
x = 4, when y = 2
Solving for the slope:


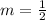
The equation is then calculated as:

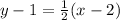

Add 1 to both sides
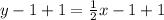

This is also true for the given expression.
Option C:
From the graph:
x = 2, when y = 4
x = 4, when y = 8
Solving for the slope:

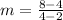
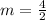
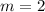
The equation is then calculated as:

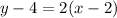
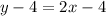
Add 4 to both sides

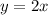
This isn't true for the given expression.
Option (D):
From the table:
x = 2, when y = 1
x = 4 when y = 3
Solving for the slope:


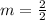
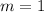
The equation is then calculated as:

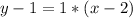
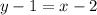
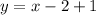
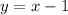
This isn't true for the given expression.