Question

A plane flying horizontally at a speed of 40.0 m/s and at an elevation of 160 m drops a package. Two seconds later it drops a second package. How far apart will the two packages land on the ground?

Answer 1

Package 1 will land at 228.0 m, package 2 will land at 308.0 m, and the distance between them is 80.0 m.

Step-by-step explanation:

To find the distance at which the first package will land we need to calculate the time:

`Y_(f) = Y_(0) + V_(0y)t - (1)/(2)gt^(2)`

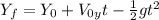
Where:

Y(f) is the final position = 0

Y(0) is the initial position = 160 m

V(0y) is initial speed in "y" direction = 0

g is the gravity = 9.81 m/s²

t is the time=?

`0 = 160 m + 0t - (1)/(2)9.81 m/s^(2)t^(2)`

`t = \sqrt{(2*160 m)/(9.81 m/s^(2))} = 5.7 s`

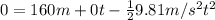
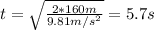
Now we can find the distance of the first package:

`X_(1) = V_(0x)*t = 40.0 m/s*5.7 s = 228.0 m`

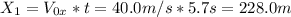
Then, after 2 seconds the distance traveled by plane is (from the initial position):

`X_(p) = V_(0x)*t = 40.0 m/s*2 s = 80.0 m`

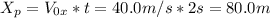
Now, the distance of the second package is:

`X _(2) = X_(1) + X_(p) = 228.0 m + 80.0 m = 308.0 m`

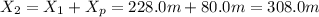
The distance between the packages is:

`X = X_(2) - X_(1) = 308.0 - 228.0 m = 80.0 m`

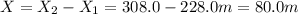
Therefore, package 1 will land at 228.0 m, package 2 will land at 308.0 m and the distance between them is 80.0 m.

I hope it helps you!