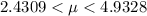Question

Compute a 99% confidence interval for the mean weight of toxic substance per gram of mold culture. State the assumption you make about the population.

Answer 1

Complete Question

The complete question is shown on the first uploaded image

Answer:

The 99% confidence interval is
`2.4309 <  \mu <   4.9328`

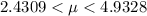
Explanation:

From the question we are told that

The data is 3, 2,5, 3, 2, 6, 5,4.5, 3, 3, and 4

The sample size is n = 11

Generally the sample mean is mathematically represented as

`\= x  =  (\sum x_i)/(n)`

=>
`\= x  =  (3+ 2+5+ \cdots +4 )/(11)`

=>
`\= x  =  3.6818`

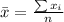
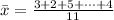
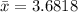
Generally the sample standard deviation is mathematically represented as

`\sigma  =  \sqrt{(\sum [ x_i - \= x ] )/(n) }`

=>
`\sigma  =  \sqrt{([ 3 - 3.6818 ]^2 +[ 2 - 3.6818 ]^2 + \cdots + [ 4 - 3.6818 ]^2   )/(11) }`

=>
`\sigma  =  1.3091`

Given that the confidence interval is 99% then the level of significance is mathematically represented as

`\alpha= (100 - 99) \%`

=>
`\alpha= 0.01`

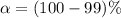
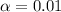
Given that the sample size is small we will making use of t distribution table

Generally from the t distribution table the critical value of at a degree of freedom of is

`t_{(\alpha )/(2) , 10 } =3.16927267`

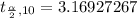
Generally the margin of error is mathematically represented as

`E =  3.16927267  *  (1.3091 )/(√(11) )`

`E = 1.251`

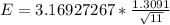
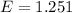
Generally 99% confidence interval is mathematically represented as

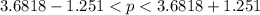
`3.6818 -1.251 <  p < 3.6818 + 1.251`

=>
`2.4309 <  \mu <   4.9328`