Question

g What is the max number of 4-element-subsets of we can select, such that intersection of any 3 of them is empty?

Answer 1

16

Explanation:

In order to get the max number of 4-element-subsets of we can select, such that intersection of any 3 of them is empty, we need to calculate the power of the set having four elements. Let the set containing the element be A as shown;

Let set A = {a, b, c, d}

Power of the set P(A) =
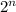`2^n` where:

n is the total number of element in the set. Since we have four elements in the set, n = 4

`P(A) = 2^4\\P(A) = 16`

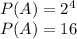
This means that the set A have 16 subsets. The subsets of the set are:

{}, {a}, {b}, {c}, {d}, {a, b}, {a, c}, {a, d}, {b, c}, {b, d}, {c, d}, {a, b, c}, {a, b, d}, {b, c, d}. {a, c, d}, {a, b, c, d}.

From all the subsets, it can be seen that intersection of set {a} and {b}, {a} and {c}, {c} and {d} are empty.

Hence the max number of 4-element-subsets of we can select, such that intersection of any 3 of them is empty is 16