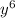Answer:
8
 + 12
+ 12
 y² + 6x²
y² + 6x²
 +
+
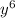
Explanation:
This can be expanded using the binomial theorem or by multiplying the factors.
In case you are not aware of the theorem, will do multiplication.
Given
(2x² + y²)³ = (2x² + y²)(2x²+ y²)(2x² + y²)
Expanding the second pair of factors
Each term in the second factor is multiplied by each term in the first factor, that is
2x²(2x² + y²) + y²(2x² + y²) ← distribute both parenthesis
= 4
 + 2x²y² + 2x²y² +
+ 2x²y² + 2x²y² +
 ← collect like terms
← collect like terms
= 4
 + 4x²y² +
+ 4x²y² +

Now multiply this by the remaining factor (2x² + y²)
(2x² + y²)(4
 + 4x²y² +
+ 4x²y² +
 )
)
= 2x²(4
 + 4x²y² +
+ 4x²y² +
 ) + y²(4
) + y²(4
 + 4x²y² +
+ 4x²y² +
 ) ← distribute both parenthesis
) ← distribute both parenthesis
= 8
 + 8
+ 8
 y² + 2x²
y² + 2x²
 + 4
+ 4
 y² + 4x²
y² + 4x²
 +
+
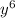 ← collect like terms
← collect like terms
= 8
 + 12
+ 12
 y² + 6x²
y² + 6x²
 +
+